AIの分野では、さまざまなアルゴリズムやモデルがデータを基に予測や意思決定を行っています。
その中で、特に「ベイズの定理」という統計学の基本的な理論が重要な役割を果たしています。
ベイズの定理は、ある事象が発生した後に、その事象がどのような原因から生じたかを推定するための方法です。
これにより、AIシステムはより正確な予測や分類を行うことができます。
ベイズの定理の基本
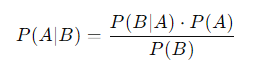
ベイズの定理の公式
- P(A∣B)P(A|B)P(A∣B):事象Bが発生したときに、事象Aが発生する確率(これを「事後確率」と呼びます)。
- P(B∣A)P(B|A)P(B∣A):事象Aが発生したときに、事象Bが発生する確率。
- P(A)P(A)P(A):事象Aが発生する確率(これを「事前確率」と呼びます)。
- P(B)P(B)P(B):事象Bが発生する確率。
この公式を使うことで、既存のデータから新しいデータの確率を計算し、モデルの予測をより精度高くすることが可能です。
ベイズの定理のAIでの活用
ベイズの定理は、特にAIの機械学習分野で広く使われています。
「ナイーブベイズ分類器」と呼ばれるアルゴリズムは、この定理を基にして動作しています。
この分類器は、スパムメールのフィルタリングや画像認識などのタスクで利用されており、膨大なデータを効率よく分類することができます。
例1: スパムメールのフィルタリング
ナイーブベイズ分類器は、メールの内容に基づいてスパムメールかどうかを判定します。
メール内の「無料」や「今すぐ」などの単語が出現する確率を事前に計算し、これらの単語が出現したときのスパムメールの確率を計算します。
この際、ベイズの定理が利用され、メールがスパムであるかどうかの判断が行われます。
例2: 画像認識
画像認識においても、ベイズの定理は重要な役割を果たしています。
AIが猫の画像を認識する際に、画像内のピクセル情報を基に、猫である確率を計算します。
過去のデータを活用し、ベイズの定理を用いて、より高い精度で猫を認識できるようになります。
ベイズの定理のメリットと課題
メリット
- 柔軟性
ベイズの定理は、データが少ない場合でも利用可能であり、事前確率を設定することで推論が可能です。
- 更新可能性
新しいデータが追加されるたびに、事後確率を更新できるため、動的な学習が可能です。
課題
- 事前確率の設定
事前確率の設定が適切でない場合、結果に大きな影響を与える可能性があります。
- 計算コスト
データが多くなると、計算コストが高くなるため、大規模なデータセットでの運用には工夫が必要です。
まとめ
ベイズの定理は、AIの予測や分類において非常に重要な理論であり、特に機械学習アルゴリズムでの活用が広がっています。
データに基づいて確率を計算することで、より正確な判断を行うことができるため、AIの精度向上に貢献しています。


